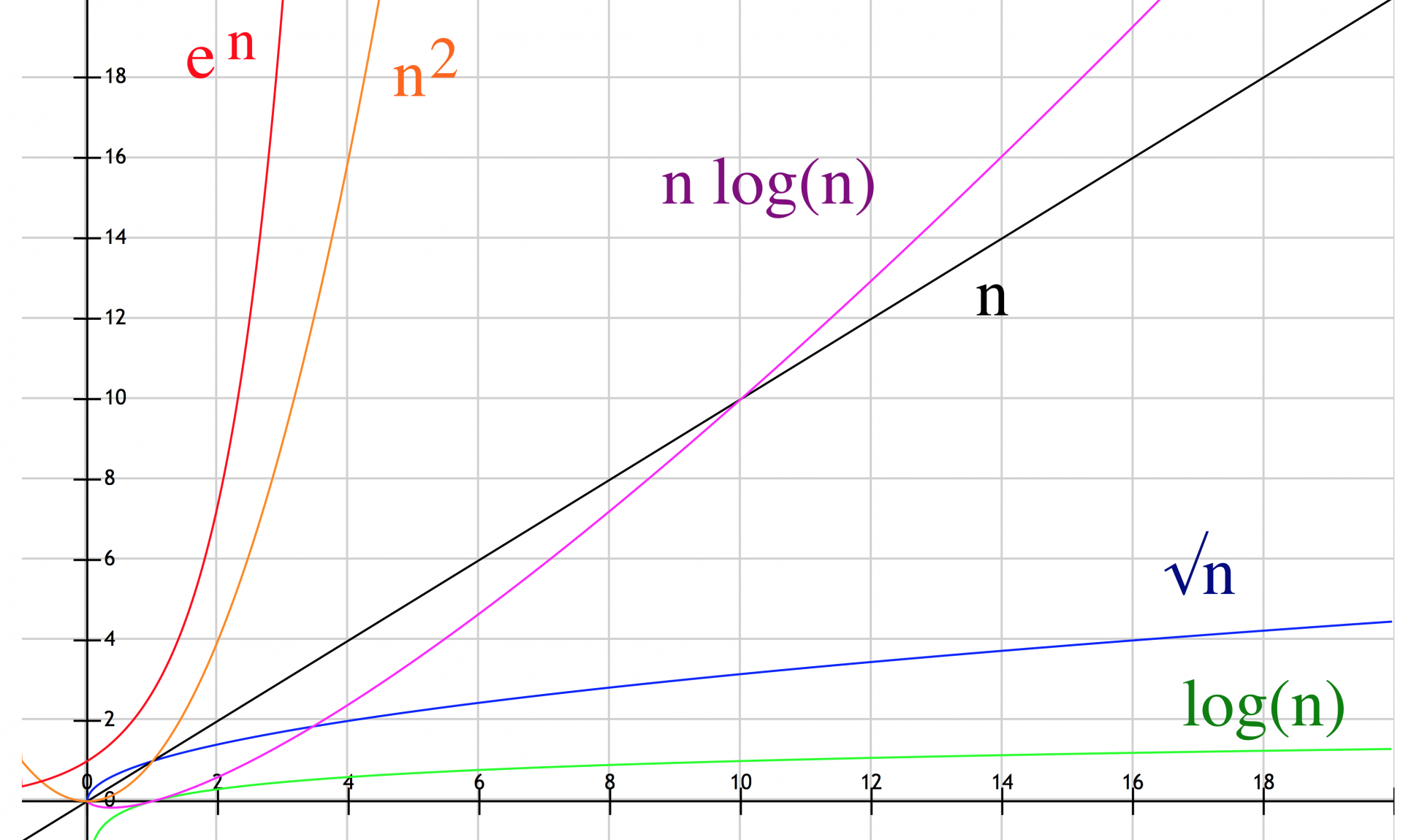
Nel primo articolo è stato introdotto il vastissimo argomento della complessità computazionale. In questa seconda parte, cercheremo di analizzare brevemente alcuni esempi pratici per comprendere meglio la notazione Big O.
Quanto segue è pensato come la naturale prosecuzione del precedente articolo, infatti non si scenderà nuovamente nei dettagli sul come avviene il calcolo del tempo di esecuzione di determinati costrutti.
Resta valida la premessa fatta precedentemente: nessuno dei due articoli sostituisce uno dei tanti validi libri dedicati a questo complesso argomento, piuttosto si vogliono fornire dei concetti di rapida comprensione che lasciano spazio ad un eventuale approfondimento a discrezione del lettore.
considerazioni generali
Le operazioni di inizializzazione, confronto ed incremento della variabile contatore nei cicli hanno un tempo di esecuzione pari ad O(1). Le operazioni di inizializzazione di una variabile, operazioni aritmetiche (moltiplicazione, addizione, etc.), accesso ad un elemento di un array, hanno anch’esse un tempo di esecuzione pari ad O(1).
Infine, anche i costrutti if di seguito elencati (poiché eseguono dei confronti semplici) hanno un tempo di esecuzione pari ad O(1).
Come spiegato nell’articolo precedente, ai fini dell’analisi Big O, sono operazioni che non hanno peso se esiste qualche operazione che ha un tempo di esecuzione dominante.
esempi
a elevato b
int power(int a, int b) {
if (b < 0)
return 0;
else if (b == 0)
return 1;
else
return a * power(a, b-1);
}
Il tempo di esecuzione è pari ad O(b) perché in totale vengono eseguite b chiamate della funzione power.
ciclo per n/2
void func(int[] arr) {
int somma = 0;
for (int i=0; i<arr.length/2; i++)
somma += arr[i];
}
Il tempo di esecuzione è pari ad O(N). Il fatto che venga effettuato un numero di iterazioni pari ad N/2 non ha impatto sull’analisi Big O.
Cicli sequenziali
void func(int[] arr) {
int somma = 0, prodotto = 1;
for (int i=0; i<arr.length; i++)
somma += arr[i];
for (int i=0; i<arr.length; i++)
prodotto *= arr[i];
}
Il tempo di esecuzione è pari ad O(N).
Poiché vengono effettuate due iterazioni complete sullo stesso array, la complessità computazionale è pari a O(2N), ma, compe spiegato nel precedente articolo, i termini costanti vanno rimossi.
Cicli annidati
void func(int[] arr) {
for (int i=0; i<arr.length; i++)
for (int j=0; j<arr.length; j++)
System.out.println(arr[i]*arr[j] + "");
}
Il tempo di esecuzione è pari ad O(N*N) –> O(N²) poiché i due cicli for sono annidati ed agiscono sullo stesso array di lunghezza N.
cicli annidati 2
void func(int[] arr) {
for (int i=0; i<arr.length; i++)
for (int j=i+1; j<arr.length; j++)
System.out.println(arr[i]*arr[j] + "");
}
Questo esempio è molto simile a quello precedente, ad eccezione del fatto che il secondo ciclo for parte da i+1. Il numero di iterazioni totali del secondo ciclo è pari a:
(N-1) + (N-2) + (N-3) + ... + 2 + 1 ---> N/2
Poiché in media il ciclo interno esegue N/2 iterazioni, il lavoro totale è pari a N²/2, quindi O(N²).
cicli annidati 3
void func(int[] arrA, int[] arrB) {
for (int i=0; i<arrA.length; i++)
for (int j=0; j<arrB.length; j++)
System.out.println(arrA[i]*arrB[j] + "");
}
Per ogni elemento di arrA, vengono eseguite b iterazioni, dove b=arrB.length. Se a=arrA.length, il tempo di esecuzione è pari ad O(ab).
ATTENZIONE a non commettere l’errore di valutarlo come O(N²), perché i due array sono diversi e potrebbero avere lunghezze diverse.
verifica numero primo
void isPrime(int n) {
for (int i=2; i<=Math.sqrt(n); i++)
if (n%i==0)
return false;
return true;
}
Il precedente blocco di codice verifica se un numero è primo controllandone la divisibilità per i numeri ad esso inferiori, fino al raggiungimento della sua radice quadrata. Il tempo di esecuzione è pari ad O(√N).
n-esimo numero di fibonacci
void fibo(int n) {
if (n<=0)
return 0;
else if (n == 1)
return 1;
else
return fibo(n-1) + fibo(n-2);
}
Generalmente, quando un algoritmo ha chiamate ricorsive multiple, ci si trova davanti ad un tempo di esecuzione esponenziale. Nello specifico, il calcolo della complessità di questo algoritmo si effettua secondo il seguente modello: O(ramiRicorsioneprofondità).
Sono presenti due rami di ricorsione per chiamata e la profondità è pari ad N.
Il tempo di esecuzione è quindi pari ad O(2N).
ricerca binaria
int binarySearch(int arr[], int x)
{
int l = 0, r = arr.length - 1;
while (l <= r)
{
int m = l + (r-l)/2;
if (arr[m] == x)
return m;
if (arr[m] < x)
l = m + 1;
else
r = m - 1;
}
return -1;
}
La ricerca binaria (che verrà spiegata approfonditamente nel successivo articolo), è un classico esempio di algoritmo con tempo di esecuzione pari ad O(logN).
Il principio sul quale si basano gli algoritmi con complessità logaritmica è quello di ridurre la dimensione del problema ad ogni iterazione. In questo caso specifico, ad ogni iterazione lo spazio di ricerca viene dimezzato. Nel caso peggiore si andranno quindi a fare log2 n iterazioni.
CONCLUSIONI
Questo secondo e breve articolo conclude l’introduzione dedicata al vastissimo mondo dell’analisi della complessità computazionale.
È importante, per uno sviluppatore, comprendere pienamente l’argomento, perché, specie quando si lavora con una grande mole di dati, la scelta di un algoritmo rispetto ad un altro può fare la differenza nei tempi di esecuzione.
Nel corso di questi due articoli sono stati introdotti i concetti teorici sui quali si basa l’analisi dei costi computazionali e sono stati analizzati alcuni esempi pratici. L’invito per i lettori è quello di continuare a documentarsi sull’argomento, magari acquistando uno dei tanti validi testi dedicati agli algoritmi.
Nei prossimi giorni arriveranno articoli dedicati ai più diffusi algoritmi.
BIBLIOGRAFIA
Cracking the Coding Interview di Gayle Laakmann McDowell.